Matematik z Harvardu vyřešil letitý kombinatorický problém šachových královen
Šachovou hádanku známou jako „problém osmi královen“ se podařilo vyřešit relativně rychle. Její rozšířené zadání pro n královen čekalo na své vyřešení dlouhých 150 let
Problém osmi dam je šachová nebo spíše kombinatorická úloha s velmi jednoduchým zadáním. Úkolem je rozmístit osm dam na šachovnici tak, aby se navzájem neohrožovaly. Tento problém poprvé zveřejnil Max Bezzl v roce 1848. Trvalo jen dva roky, než Frank Nauck správně vypočítal počet řešení – osm královen lze na klasické šachovnici rozmístit v celkem 92 rozestaveních, aniž by se mezi sebou ohrožovaly.
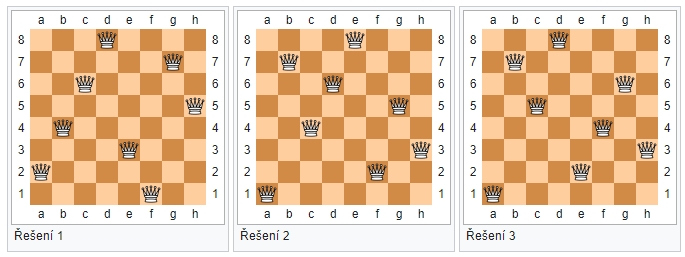
Vedle řešení původního zadání přišel Frank Nauck s novou výzvou zobecněnou jako „n dam na n rozměrné šachovnici“. Toto zadání se ukázalo jako mnohem tvrdší oříšek. Americký institut Clay Mathematics Institute dokonce v roce 2017 nabídl rovný milion dolarů tomu, kdo dokáže napsat algoritmus pro rychlé řešení „problému osmi královen“, nebo dokáže, že je problém neřešitelný. Nauckova výzva zůstávala bez řešení až do loňského roku. Téměř úplným pokořitelem problému n dam se nakonec stal matematik Michael Simkin z centra Center of Mathematical Sciences and Applications na americkém Harvardu.
Řešení pro n dam
Simkin spočítal, že pro n dam na n rozměrné šachovnici existuje zhruba (0,143 × n) ⁿ řešení. Tento výsledek není dokonale přesnou odpovědí, ale přibližuje nás k ní, jak to jen se současnou úrovní vědomostí a matematických nástrojů dokážeme. Pro matematiky je to přijatelné řešení problému.
TIP: Kolik je v jedné šachové partii možných tahů? Více než atomů v pozorovatelném vesmíru!
Pro představu, pokud bychom měli gigantickou šachovnici s milionem políček na každé ze stran, na kterou bychom měli umístit milion královen, nejprve bychom toto číslo vynásobili 0,143, čímž dostaneme 143 000. Takové číslo je ještě víceméně představitelné. V druhém kroku ale následuje umocnění čísla 143 000 na 1 milion, jehož výsledkem je monumentální cifra s 5 miliony číslic.





